by Alice Humphrey
1. Introduction
Geometric ornamental decoration is found on every-day, functional objects as well as elite items. It appears deceptively simple and can often be executed without a high degree of skill or training but many ethnographic case studies have identified concepts of ‘right’ and ‘wrong’ in geometric decoration indicating that its construction is, in some cases controlled by a set of, sometimes complex, underlying rules which may not be consciously articulated but which provide a valuable source of information about technology, mathematical knowledge and even social structure (Herner 1989, Eglash 1999, Fischer 1961). The proposed method suggests a consistent means of recording geometric motifs. In spite of their potential research value, the search for objects to analyse during this research highlighted that geometric decoration is often under-recorded in textual descriptions of objects, particularly when representational decoration is also present.
2. Choice of Approach
The method put forward in this paper captures the structure of geometric ornament in a numerical form which allows bottom-up classification on a graduated similarity scale. Motifs described by this approach were subsequently classified by cluster analysis. This method is contrasted with a commonly applied classification system based on mathematical spiral types.
The method was developed to assess whether the characteristics of individual types of geometric motif provided a relevant dataset for use in cross-cultural comparison of decorative style. In application, ornamental spiral forms present in the decoration of four prehistoric or early-historic cultures for which there is no evidence of direct contact or cross-influence were analysed (Shang Dynasty to Eastern Zhou Period China; Early to Late Jōmon Japan; Middle Kingdom and Second Intermediate Period Egypt; and Bronze Age Cyprus c.1600-600). The study aimed to identify, by comparison with instances of naturally occurring spirals, whether the inspiration for the production of spiral motifs was associated with a particular natural origin and, if so, whether this inspiration was culture-specific or could be suggested to transcend cultural boundaries.
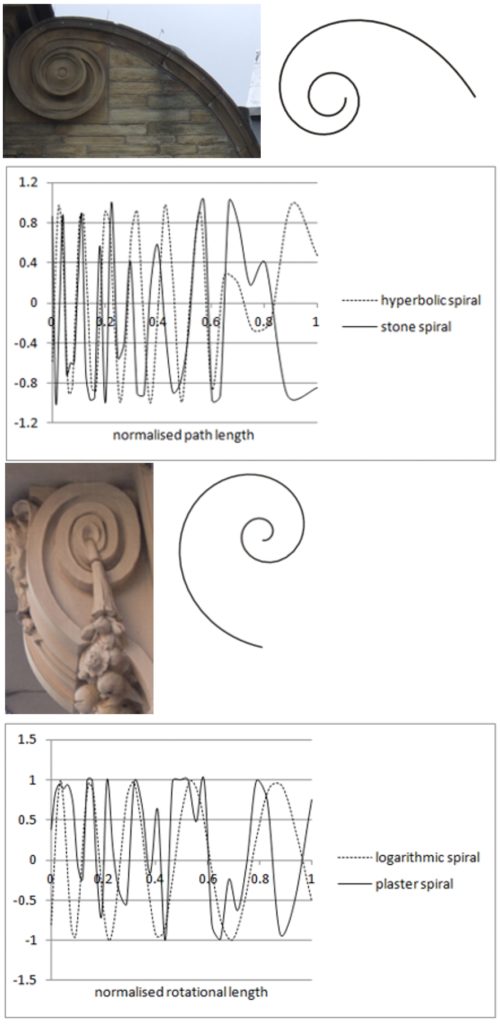
Previous studies of ornamental spirals have used visual estimation of similarity to mathematical spiral types as a means of classifying them (e.g. Zhuschikhovskaya & Danilova 2008; Fuchigami 2001). However, in spite of apparent visual similarity between decorative and mathematical spiral forms, measurement can show the match to be poor; Figure 1 (top) shows the aberration in the sine wave of the decorative spiral which visually resembles a hyperbolic spiral compared to the sine wave of a true hyperbolic spiral. Decorative spirals also often show similar correlations with more than one mathematical spiral type (Andrey & Galli 2004). An additional problem in assigning decorative spirals to mathematical type classes lies in the need to discount visually significant elements of the motifs, such as tapering of the spiral line and distortions in curvature. Figure 1 (bottom) shows the greater difference between a true logarithmic spiral and a visually approximated form produced by even a relatively slight distortion in curvature.
Figure 1 top: Architectural stone spiral (on the former Windsor Baths, Bradford, built in 1905) approximated to a hyperbolic spiral form; bottom: architectural plaster spiral (Leeds) approximated to a logarithmic spiral form.
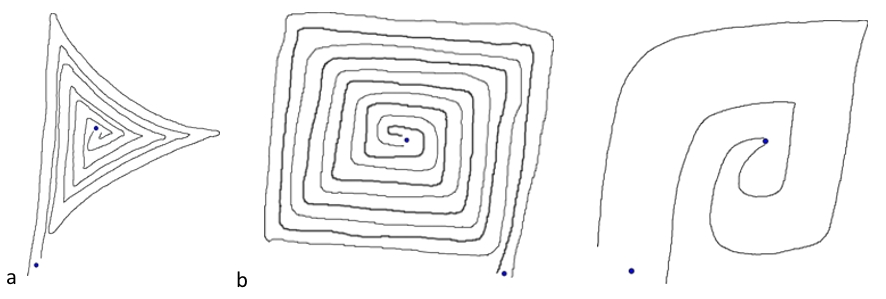
Loehr’s (1953; 1968 cited in Chang 1980 pp.28-30) classification system of Shang Dynasty vessel types allocated some spiral motifs exclusively to particular decorative subgroups. In comparison with Loehr’s classification, the classifications derived from correlation to mathematical forms (Figure 2a) tended to overly merge classes whereas those derived by applying the method proposed in this paper and applying cluster analysis (Figure 2b) tended to over segregate classes.
Figure 2a: Classification of the spirals in the Shang Dynasty/Western Zhou Period case study according to Pearson correlation with the spectral density of mathematical spiral forms.

Figure 2b: Classification of the same sample applying cluster analysis on the proposed method of description.

Cluster analysis was found to be more effective in drawing together spirals which deviate strongly from a broadly circular outline (Figure 3a). Both methods were equally effective in separating the open spirals of low rotation from the tight spirals of high rotation and with drawing together spirals with a known representational meaning (Figure 3b).
Figure 3: A- the exemplar spiral with a strong visual difference from any mathematical spiral types from a Western Zhou Period gui (ritual vessel); B-exemplar spirals, from Shang Dynasty and Western Zhou Period bronze vessels, with known representational meaning – leiwen, (‘thundercloud’ spirals); and the horn of the mythical creature known as a taotie.
The fundamental problem with the mathematical class system is that detailed assessment shows that the apparent resemblance to mathematical spiral types is superficial. Therefore the use of mathematical terms creates false implications about shape; forces conformity to artificial external groupings; and implies false precision in analysis and in the construction of the decoration.
The clustering method creates class divisions but also creates a graduated ranking of similarity that runs across the full sample as shown in figure 2b. In application to the Shang Dynasty/Western Zhou Period case study, this gradual change was the most striking aspect of the clustered results, represented as a graduation from widely spaced background spirals of low rotational length and constant expansion rate through representational spirals with increasing expansion rates; to spirals of low spacing, high rotational length and constant expansion rate. This suggests that absolute class grouping is not the most appropriate form of classification of the motifs. Decorative motifs particularly tend towards this type of graduation since there are no practical constraints to which they must conform to be able to fulfil a function. However, striking breaks in the graduated scale might indicate divisions of type that are identifiable to the producers and consumers of the decoration.
Creating ranked similarities through qualitative assessment would be a slow process and it is unlikely that, even with expert assessors, there would be complete agreement. A numerical descriptive approach provides consistency in the creation of type assessments on a continuous gradient both at an inter- and intra-sample level. It also provides a numerical measure of the degree of similarity between motifs which is useful in making comparisons with numerical contextual data; for example in assessing rate of change over time and in highlighting striking breaks in the graduated similarity scale.
In opposition to the argument proposed above, that the exclusion of human assessment from ranking of similarity makes the process quicker and more consistent; it must be noted that quantification loses the relevant contextual knowledge which allows experts in the field to make valid judgements to prioritise one feature over another and to create typologies drawing on the knowledge of the full decorative scheme of the object. Because of this it is suggested that this method should be used in conjunction with appraisal of the broader decorative scheme and that it is particularly relevant in cross-cultural studies where assessments are not based on the in-depth knowledge of a single culture.
Within the context of a multi-method study, the quantification of motif shape facilitates the isolation of individual attributes of a motif for comparison. This allows attributes to be compared between different motifs where appropriate and to bring out the fine detail of individual motif types which might otherwise not be noted as significant.
Figure 4: Distributions of rotational length and curvilinearity attributes in the four case study cultures.
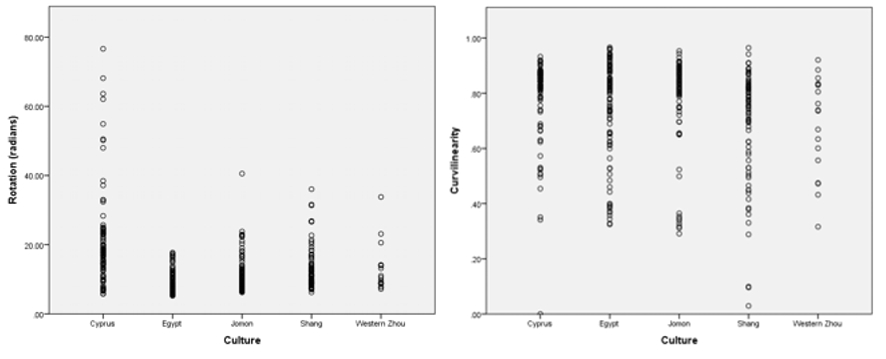
This proved to be significant within the spiral case study where no clear patterns were found in the aggregate data distribution but separate assessment of rotational length and curvilinearity highlighted a remarkable consistency in motif structure amongst the cultures (Figure 4). Both of these areas of similarity would accord with natural spiral structures being an important source of inspiration for decorative spirals. That the Cypriot sample shows a greater variance in rotational length, possibly indicates that technological knowledge – coiled wire spirals and wheel-turned pottery influenced the style of the motifs. The segregation of individual variables can also be useful in identifying culturally important variables in studies where access to informants is not available by highlighting those with non-random distributions. In contemporary ethnographic examples, the isolation of variables offers a means of discriminating and quantifying differences identified through interview. If a numerical basis can be established for reported preferences or groupings then these values can be used to look at other aspects of the culture to search for similar preferences. Adams (1973), in a study of Sumba ceremonial dress, found that the structures present in the decoration of were also reflected in language structure and in settlement layout.
3. Digital Techniques in the Application of the Method
In the current implementation of the method, the internal and external outline of the motif is traced from a photograph using a digitisation tablet (Figure 5). These tracing lines are recorded as Cartesian coordinates and serve as the basis for the subsequent description and analysis using a JavaScript applet within the interactive geometry programme Geogebra.
Figure 5: An ornamental spiral from a Chinese Eastern Zhou Period you (ritual wine vessel).
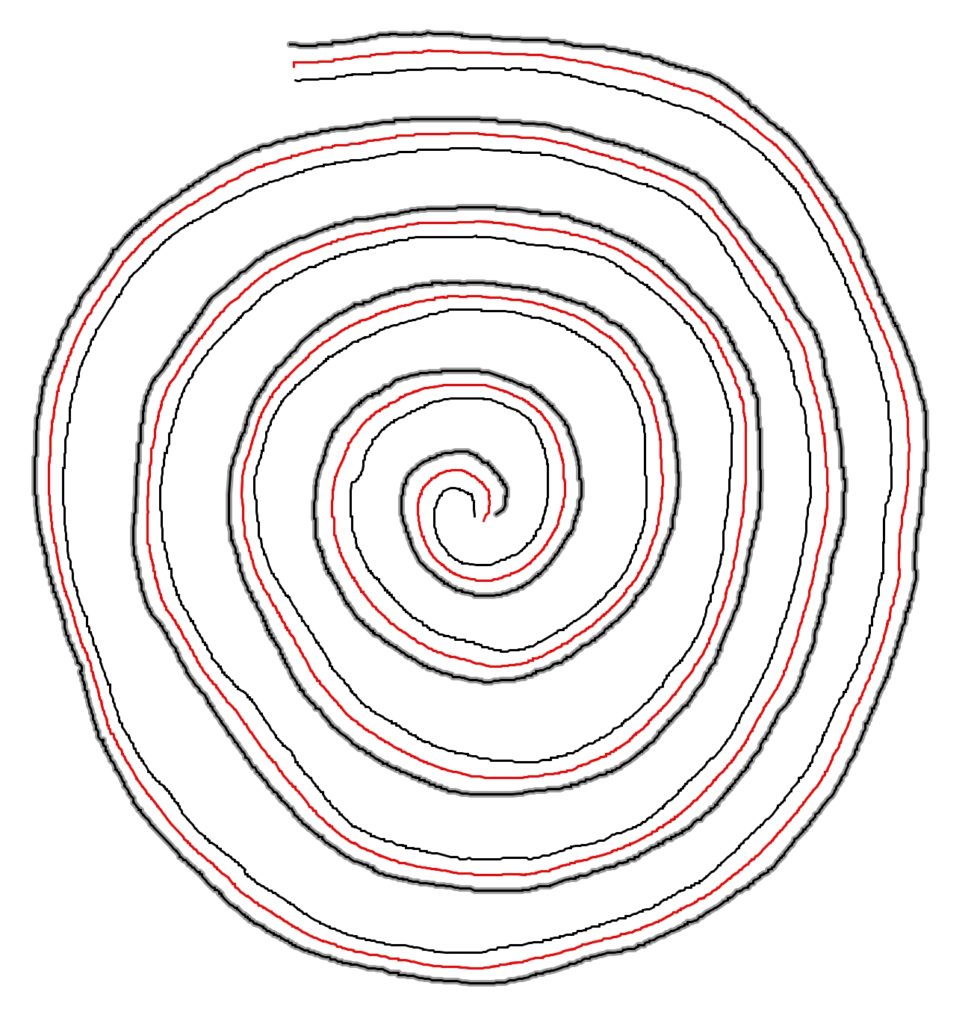
The applet automated the creation of a centre line of the spiral (shown in red on Figure 5) quantified as a sequence of tangent angles measured at constant rotational intervals around the spiral. This was then converted into a sine wave (Figure 6a). The spectral density plot of the Fourier transform of the sine values (Figure 6b) was used in the subsequent comparative analyses by creating correlation scores for the plot of each spiral with all other spirals in the sample.
Figure 6: A- the tangent sine values of the spiral shown in Figure 5; B- the spectral density plot of the Fourier transform of the sine values.

The second stage of analysis combined the correlation values with variables quantifying the more stylistic aspects of the motifs. These variables included one which was specific to the motif type – spacing between coils alongside more broadly applicable variables of path width, irregularity, curvilinearity, orientation, rotational length and maximum diameter. Cluster analysis was applied to the combined variable set to rank the similarity of the spirals and to create class groupings.
4. Digital Techniques in Data Distribution and Cataloguing
In practical application, the software used in this method has the advantage of wide availability. The method can be entirely implemented using a combination of freeware and Excel and the outlines of the motifs can be easily reconstructed from the numerical description by entering the tracing coordinates into a CAD programme. It is planned that the analysis applet and the accompanying Excel macros for pre-processing the data will be made available online for direct application to spiral motifs or for adaptation to different motifs by modification of the code.
The main time expenditure within analysis is in tracing the motifs. This usually requires human input because there is not sufficient contrast for automated edge detection. Possibly this aspect of the analysis could offer an opportunity for crowd sourced input in future if a large enough dataset were assembled to warrant it.
As currently implemented, the method is customised to the analysis of spiral forms. However, the underlying principles of the method would be applicable to a number of other geometric constructs and visually simple discrete motifs. In analysing spirals, it was necessary to apply subjective limits to some aspects of the fundamental definition of what constitutes a spiral, such as defining a minimum rotational length. This led to the exclusion of some motifs which were on a visual continuum with the analysed spirals such as ‘false spirals’ – sets of concentric circles linked by diagonal lines to resemble a running spiral design. It is hoped that the future expansion of the method to increase the range of analysable motifs may increase the flexibility of the system and go some way to address this limitation.
In the context of the collation of motif descriptions in databases, it is only necessary for the format of the data to be consistent. For example, a researcher wishing to study tool markings might use the raw data of this study in the form of Cartesian coordinate outlines, obtained by tracing and discounting the style related measures derived from these, as not relevant to their study. They might then supplement the data with their own coordinate outlines obtained using edge detection software to add to both their study and to the database.
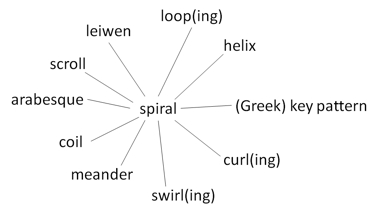
The standard manner of description of geometric ornament in databases is within a free text field or by keywords. When described in this manner, the ubiquity of geometric ornament acts against its easy retrieval in that there are numerous different specialist or colloquial terms which can be used to describe a single construct (Figure 7) making comprehensive searching difficult.
Figure 7: Terminology encountered in museum catalogues and journal papers for describing spiral decoration.
A shape-matching search method using numerical shape descriptions can circumvent these difficulties. Shape matching algorithms have been used on prehistoric petroglyphs and on lithic outlines for example, a method proposed by Xi, Keogh, Wei and Mafra-Neto (2007) which operates on tangent sine measurements and could be applied to the spiral centre line data. Another method, by Dey, Giesen and Goswami (2003), uses Cartesian coordinates. The ability to reconstruct the motif as a vector image means that other shape matching algorithms could equally be applied. The facility for incorporating a shape matching method into a database of numerical motif descriptions held in a compatible format would be a highly beneficial feature taking full advantage of the potential power of numerical description as a terminology-independent searching and cataloguing tool.
Two possible approaches are therefore proposed. The first is the creation of a new database which would facilitate the collation of large data sets with motif structure acting as the primary theme. This would allow cross-cultural searches outside standard culture groupings to be made and would facilitate the implementation of shape-matching search techniques.
The alternative approach would be the addition of numerical descriptions to existing databases and museum catalogue records, for example as text or comma separated variable files. This would require little additional storage space. As well as being a good means of distributing data by getting it onto already well known and accessed catalogues; the repetition of cataloguing work entailed in the creation of a new database would be avoided. The likelihood of obsolescence and non-maintenance of the database, also a potential drawback of the creation of a new database, would be reduced.
If, however data were spread across the databases of disparate museums, then collated data would be less easily retrieved and motif records for objects without a public catalogue record would be unavailable. The possibility of searching by shape-matching techniques, one of the key advantages of numerical description as a database tool, would also be lost. It is likely that institutions maintaining existing catalogue records would need to see evidence of the utility and use of the new datasets before being prepared to support them.
The key challenge, whichever data collation method is tried, will be building up sufficient interest in using, and adding to, numerical motif descriptions to generate a sample size that returns useful results and maintains momentum.
5. Conclusion
The method proposed in this paper is designed to describe geometric ornament numerically using a consistent standard in the form of raw shape descriptions. In testing the method on a set of spiral motifs it proved to be a more flexible and appropriate classification system than the often used reference to mathematical spiral types and it highlighted some striking consistencies in the shape of spiral motifs across four cultures with no evidence of direct contact.
The strengths of the method lie in its capacity to produce a classification derived from within the sample rather than externally imposed, and that it is one which can quantify gradations of difference. Because of the focus of this method on describing and analysing the detail of motif structure, it excludes broader context from consideration within the method. So it is best suited to form one component of a mixed methods research project.
Geometric ornament is an area which has the potential for greater exploration and which often goes unrecorded particularly as a systematic, rather than a free text, description. Numerical shape description offers the possibility of searching for data without dependence solely on textual description. It has the potential to open up access to large datasets of geometric ornament in a format which facilitates quantitative analysis, and which can grow as further research is carried out.
References
Adams, M.J. 1973. Structural aspects of a village art. American Anthropologist 75:1:265-279.
Andrey, D and M. Galli. 2004. Geometric Methods of the 1500s for Laying Out the Ionic Volute. Nexus Network Journal [online] 6:2:31-48, [accessed 5.1.2010]. Available from: http://www.nexusjournal.com/.
Chang, K.-C. 1980. Shang Civilization. London: Yale University Press.
Dey, T.K., J.Giesen and S.Goswami. 2003 Shape Segmentation and Matching with Flow Discretization. Proceedings of the 8th International Workshop on Algorithms and Data Structures (WADS), Lecture Notes in Computer Science 2748 25-36.
Eglash, R. 1999. African Fractals: modern computing and indigenous design. New Brunswick: Rugers University Press.
Fischer, 1961. Art styles as cultural cognitive maps. American Anthropologist. 63:79-93.
Fuchigami, K. 2001. Analysis of the spiral pattern karakusa. Journal for Geometry and Graphics. 5:1:35-43.
Herner, E. (trans. A. CROZIER) 1989. Spiral Decoration in Early Bronze Age Scandinavia: A Technical and Qualitative Analysis and Study of Production. British Archaeological Reports: International Series 552.
Jernigan, 1986. A non-hierarchical approach to ceramic decoration analysis: a Southwestern example. American Antiquity. 51:1:3-20.
LOehr, M. 1953. The bronze styles of the Anyang Period (1300-1028 B.C.). Archives of the Chinese Art Society of America. 7:42-53.
_________. 1968. Ritual vessels of Bronze Age China. New York: Asia House.
XI, X., E.Keogh, L.Wei and A. Mafra-Neto 2007. Finding Motifs in a Database of Shapes in Proceedings of SIAM International Conference on Data Mining (SDM ’07).
Ward, W.A. 1987. Scarab typology and archaeological context. American Journal of Archaeology 91:4:507-532.
Washburn, D.K. 1983. Symmetry analysis of ceramic design: two tests of the method on Neolithic material from Greece and the Aegean. in D.K.Washburn (ed.) Structure and Cognition in Art. Cambridge: Cambridge University Press, pp. 1-7.
Zhushchikovskaya, I and O. Danilova. 2008. Spiral Patterns on the Neolithic Pottery of East Asia and the Far East. Documenta Praehistorica [online] XXXV:215-226, [accessed 18/3/10]. Available from: http://arheologija.ff.uni-lj.si/documenta/.